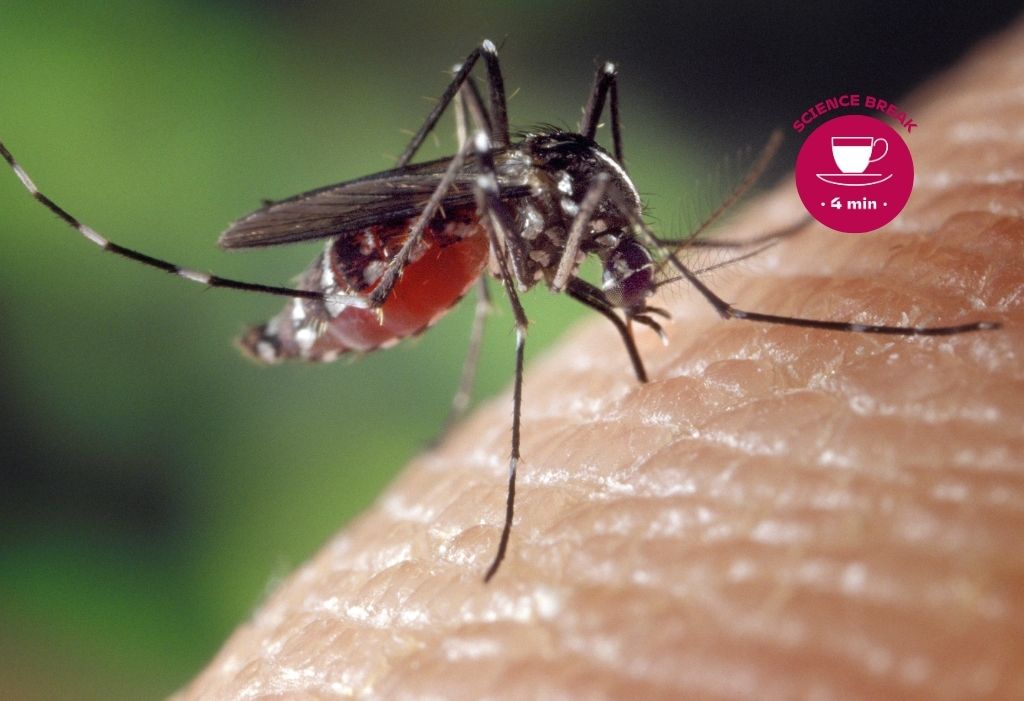
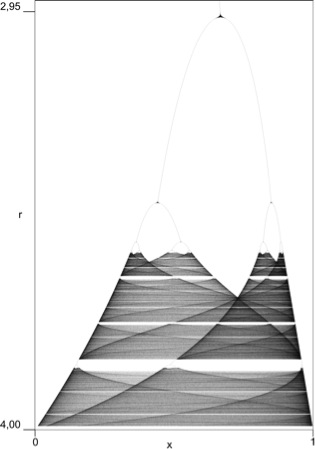
Il 25 maggio 2009 il Museo Civico di Rovereto, nell’ambito della manifestazione Discovery on film e delle sue attività di divulgazione del pensiero scientifico, inaugurava, nelle sale espositive che circondano il planetario, “La Città Elettronica (vita e morte della città)” di Francesco Cocco e Remo Forchini. Un’opera d’arte realizzata grazie a un complesso lavoro didattico che ha visto il Centro di Formazione Professionale “G. Veronesi” coinvolgere gli allievi del corso di elettronica e meccatronica in un’iniziativa artistica che ha offerto ampi spunti di riflessione raccontando l’evoluzione della città come forma e concetto, tra arte e scienza. Partendo da materiale elettronico di risulta si è voluto riprodurre la struttura e l’evoluzione di una città moderna unendo tecnica, informatica, effetti sonori ed estetici per poi proporli al pubblico che visita il planetario del Museo Civico. Dopo un’emozionante presentazione tra musica e luci, che segnano le forme e le dinamiche della crescita della città, Francesco Cocco spiega con queste parole ciò che il visitatore ha visto: “La nascita della città avviene con disegno urbano intenso e significativo, delimitato da mura, che la proteggono. Nel tempo con il passare dei secoli, inizia un’espansione sempre più veloce e incontrollata. L’enorme sviluppo demografico, avvenuto nell’era moderna in tutto il mondo, ha accelerato la totale distruzione del concetto originario della città. La sua precisa forma, quale diretta emanazione dello stato sociale ed economico, si dissolve in una dimensione illimitata, quasi una transizione dall’ordine al caos, divorando l’intero territorio.  La città si espande, si espande in ogni direzione, come lava inarrestabile, senza più nessun centro organizzativo e vitale, disperdendo così la sua forma urbana. Al cessare della forma cessa anche la vita sociale, l’equilibrio dei rapporti tra le cose e gli uomini. Per un eccesso di grandezza la città si polverizza e muore”. A questo punto sorge spontanea una domanda: che cosa lega la città elettronica e la riflessione di Francesco Cocco sulla forma della città, quale diretta emanazione dello stato sociale ed economico nelle sue varie fasi di sviluppo, con la scienza, la natura e le forme dell’universo? Non è semplice rispondere e spiegare così le ragioni dell’entusiasmo con cui abbiamo sostenuto il progetto, favorendone anche l’esposizione al pubblico, ma cercherò di farlo raccontando due esperienze che possono meglio far comprendere le ampie riflessioni didattiche, artistiche e scientifiche che l’opera stimola. Alla metà degli anni ’80, dopo la pubblicazione da parte del matematico Benoit Mendelbrot del suo lavoro sulla geometria frattale della natura (The Fractal Geometry of Nature, 1985), molti naturalisti si occuparono di caos e di geometria frattale perché cominciarono a intuire che molte forme naturali come le nubi, gli alberi, i cavoli, le suture delle ammoniti e molto altro si potevano descrivere e rappresentare matematicamente come dei frattali. In altre parole si vedeva la possibilità di superare il concetto che la natura operasse essenzialmente in modo casuale scoprendo che i sistemi naturali non hanno un comportamento totalmente casuale, ma nascondono una forma di ordine molto sottile. La teoria del caos e la nuova geometria frattale, che si basa sui principi dell’interattività infinita e dell’autosimilarità* delle figure ha quindi aperto nuove riflessioni suggerendo che vi è ordine nel caos e anche se questo pone apparenti limitazioni alla prevedibilità dei fenomeni, sembra suggerire relazioni causali dove prima non sembravano possibili. Il mondo naturale si può quindi rappresentare ora attraverso sistemi ordinati che seguono comportamenti lineari, ora attraverso sistemi complessi regolati dal caos dove, come affermava Poicaré, “una causa piccolissima che sfugga alla nostra attenzione determina un effetto considerevole che non possiamo mancar di vedere e allora diciamo che l’effetto è dovuto al caso”. Osserviamo un fluttuare continuo tra ordine e caos, alle volte cogliendo aree di transizioni e scoprendo strani attrattori e ordine in sistemi diversissimi fra loro come l’atmosfera, un rubinetto che gocciola e il battito del nostro cuore. La prima analogia con la Città elettronica vuole quindi essere la rappresentazione di strane attrattive del caos rappresentandole graficamente dopo elaborazioni al computer e su un esempio che volutamente non ha nulla di naturale. Ripropongo quindi un semplice programma al calcolatore, descritto da A.K. Dewdney nel 1987 su Le Scienze n.229, dove si parla di caos descrivendo un sistema a tre amplificatori. Supponiamo che il primo amplificatore dia in uscita il segnale x che viene passato agli altri due. Il secondo amplificatore da in uscita il segnale 1-x e il terzo assume in ingresso i due segnali x e 1-x e genera il loro prodotto x(1-x) e lo passa al primo amplificatore che riceve anche una tensione di controllo r.  Scrivendo un semplice programma che calcoli l’equazione iterata per x<--rx(1-x) con valori iniziali di x maggiori di 0 e minori di 1 e con r che oscilla tra 2,9 e 4, il circuito, formato dai tre amplificatori, esegue una “danza di tensione”, visualizzata nell’immagine che segue, che diventa sempre più sfrenata con l’aumento della tensione di controllo r.  
Per valori di r inferiori a 3,56 gli attrattori sono formati da pochi punti che rappresentano un comportamento ordinato esattamente come descritto nella nascita della città elettronica dove Francesco Cocco ricorda che “La nascita della città avviene con disegno urbano intenso e significativo (ordinato)”, mentre con l’aumentare di r da 3,56 a 4 le linee, che prima si biforcavano ordinatamente (secondo la potenza di 2; 2, 4, 8, 16), diventano una folle alternanza di punti bianchi e neri istaurando un regime caotico. Come si vede nell’immagine di tanto in tanto il regime caotico scompare e ricompaiono attrattori di biforcazione fino alla definitiva transizione al caos. Anche nella “Città Elettronica” troviamo le medesime analogie “La città si espande ….. disperdendo la sua forma urbana…. finché per un eccesso di grandezza la città si polverizza e muore” segnando così la transizione tra ordine e caos. Il diagramma di biforcazione che il computer disegna, iterando una semplice equazione, mostra la medesima transizione al caos e la rappresentazione grafica che ne deriva, esteticamente interessante, con curve e pieghe sapientemente ombreggiate, quasi fatte da un pittore esperto, attira la nostra attenzione esattamente come nella Città Elettronica. Sembra incredibile che il comportamento generale come pure l’eleganza di un particolare della biforcazione per valori di r da 2,99 a 3,01, sia generato da un’iterazione di un’equazione semplicissima. Il nostro stupore poi aumenta quando notiamo le straordinarie analogie tra la rappresentazione di azioni umane o genericamente definite biologiche con quelle riferite al mondo inorganico. Infine rimaniamo sorpresi quando ambedue i prodotti, sia quelli frutto dell’ingegno umano o semplice risultato d’iterazione matematica, trovano la loro spiegazione matematica nella teoria del caos.
La seconda riflessione prende lo spunto da un lavoro di un fisico, dell’Università dell’Oregon appassionato d’arte, Richard P. Taylor che nel 1999 pubblicò su Nature un’interessante analisi sulla pittura di Jackson Pollock (Taylor R.P., Micolich A.P. e Joans D., Fractal Analysis of Pollock’s drip painting, Nature 399, p.422, 3 giugno 1999) ripresa poi anche dalle Scienze nel numero di gennaio 2003. La storia di Taylor è singolare! Data la sua passione per l’arte s’iscrisse alla Manchester School of Art, in Inghilterra, dove è risaputo che gli studenti devono dare prova di cavarsela da soli. Nel 1994 la scuola spedì gli studenti, e con loro anche Taylor, nella brughiera dello Yorkshire dando una settimana di tempo per dipingere ciò che avevano visto. Purtroppo il maltempo rese il compito impossibile e quindi Taylor decise di lasciare che fosse la natura a dipingere per lui. Assemblò una grande struttura in legno che, mossa dal forte vento, faceva oscillare una serie di contenitori di colori che gocciolavano tracciando un disegno corrispondente alla traiettoria del vento su una tela posta per terra. Il giorno dopo, cessata la bufera, quello che rimase impresso sulla tela somigliava in modo impressionante a un dipinto di Pollock. Improvvisamente, i segreti dell’arte di Jackson Pollock sembravano svelarsi: erano i ritmi della natura quelli che seguiva quando dipingeva. Fu questo lo spunto che stimolò Taylor a studiare scientificamente le opere di Pollock scoprendo, da fisico e grazie all’analisi al computer, la presenza di schemi frattali nei dipinti dell’artista.
Taylor studiò attentamente i quadri di Pollock ricoprendo i dipinti con un reticolo, generato al computer, di celle quadrate a scala via via più grande. Osservò che gli schemi a scale diverse mostrano le stesse qualità generali indipendentemente dalla disposizione e dalle dimensioni delle celle. Poiché le qualità statistiche dei frattali si ripetono a diversi ingrandimenti, la dimensione frattale D non cambia al variare dell’ingrandimento confermando il concetto di autosimilarità. Pollock, di fatto, disegnava dei frattali e quindi la dimensione frattale D rimaneva costante su tutto il quadro. Taylor scoprì inoltre che la dimensione frattale D nei quadri di Pollock aumentava, nel corso del decennio in cui egli dipinse con la tecnica del gocciolamento, passando da 1,12 a 1,7 e permettendo a Taylor di individuare un metodo per datare con precisione e autenticare molti lavori di Pollock. A questo punto Taylor, assieme a un gruppo di psicologi esperti nella percezione visiva, volle verificare se ci fosse un valore di D universalmente preferito dall’osservatore. Nel test di percezione visiva che né seguì i partecipanti hanno coerentemente espresso una preferenza per valori di dimensioni D tra 1,3 e 1,5 indipendentemente dall’origine degli schemi frattali. Questo ci fa meglio comprendere perché quando guardiamo un’opera di Pollock rimaniamo affascinati ma la stessa sensazione non l’abbiamo ammirando una tela in cui noi stessi abbiamo fatto gocciolare del colore. Jackson Pollock dipingeva frattali venticinque anni prima della loro scoperta scientifica dimostrando che l’arte anticipa la scienza e noi tutti percepiamo la grandezza della sua opera perché lui dipingeva cogliendo i ritmi della natura di cui noi siamo parte. Anche il pulsare ritmico dei led della Città Elettronica che mostra la transizione dall’ordine al caos, vuole cogliere e descrivere l’evoluzione della città come un prodotto culturale dell’uomo, ma con un’espressione artistica che si sviluppa seguendo i ritmi della natura e con un linguaggio matematico regolato dalla teoria del caos. Per questo la visione è piacevole e nessuno, tra i molti visitatori che hanno ammirato l’opera, nelle sale del planetario del Museo Civico l’ha percepita come corpo estraneo.

*Un oggetto è autosimile quando può essere diviso in un certo numero di parti simili alla figura intera.

Didascalie delle illustrazioni

1. Diagramma di biforcazione che mostra la transizione al caos.
2. Particolare della biforcazione per valori di r da 2,99 a 3,01.
3. Autumn Rhythm, Number 30 (1950). Vernice su tela, realizzato con la tecnica del dripping (266,7 x 525,8 cm). Attualmente è conservato al Metropolitan Museum of art.